Question

Find three consecutive integers such that the sum of the first and twice the second is 104 minus three times the third.The smallest integer is

Answer 1

From the question, w hneed to translate the wording part into algebraic form as follows:

1. Three consecutive integers can be written as follows:

`x,x+1,x+2`

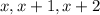
2. The sum of the first and twice the second:

`x+2(x+1)`

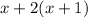
3. That sum is equal to 104 minus three times thegthird:

`104-3(x+2)`

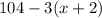
4. Therefore, we can gather all of the information - translated into algebraic form as follows:

`x+2(x+1)=104-3(x+2)`

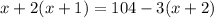
5. Now, we have to apply the distributive property on both sides as follows:

`\begin{gathered} x+(2)(x)+(2)(1)=104+(-3)(x)+(-3)(2) \\ \\ x+2x+2=104-3x-6 \\ \\ \text{ Adding like terms, we have:} \\ \\ (x+2x)+2=(104-6)-3x \\ \\ 3x+2=98-3x \end{gathered}`

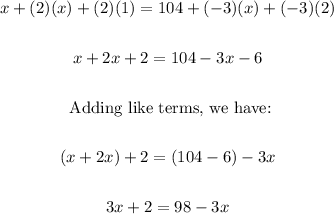
6. We need to add 3x to both sides of the equation as follows:

`\begin{gathered} 3x+3x+2=98-3x+3x \\ \\ 6x+2=98 \\ \\ \end{gathered}`

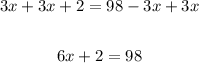
7. Now, we can fsubtract 2 from both sids of the equation, and then divide both sides by 6:

`\begin{gathered} 6x+2-2=98-2 \\ \\ 6x=96 \\ \\ (6x)/(6)=(96)/(6) \\ \\ x=16 \end{gathered}`

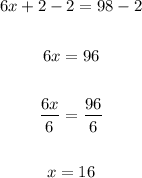
Since we have 16, this is the smallest integer. The other ones are 16+1 = 17, and 16+2 = 18, and we can check this from the equation we wrote above:

`\begin{gathered} x+2(x+1)=104-3(x+2) \\ \\ 16+2(16+1)=104-3(16+2) \\ \\ 16+2(17)=104-3(18) \\ \\ 16+34=104-54 \\ \\ 50=50 \\ \end{gathered}`

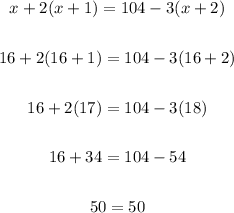
And since we got that this rhsult is always true, we can conclude, therefore, that the smallest integer is 16 (the other ones are 17 and 18).

In summary, therefore, the smallest integer is 16.