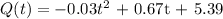Question

The following table gives the number of worldwide cell phone subscribers, in billions, for selected years from 2010 and projected to 2020. Year 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 Subscribers (billions) 5.39 6.03 6.61 7.18 7.65 7.98 8.32 8.57 8.73 8.94 9.03. Find a quadratic function that models the number of subscribers, Q(t), in billions, as a function of t, the number of years after 2010.

Answer 1

The quadratic equation is;

`Q(t)=-0.03t^2\text{ + 0.67t + 5.39}`

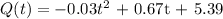
Here, we want to model a quadratic equation.

Mathematically, since in this case, t will be our independent variable while Q(t) will be the dependent variable, the quadratic function will take the form;

`Q(t)=at^2\text{ + bt + c}`

Now, when t = 0 , Q(t) = 5.39

This is the year 2010

Thus, at t = 0, we have;

`\begin{gathered} 5.39=a(0)^2\text{ + b(0) + c} \\ \\ 5.39\text{ = 0 + 0 + c} \\ \\ c\text{ = 5.39} \end{gathered}`

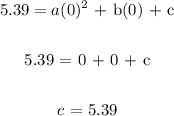
We are now left with finding a and b

In the year 2011, t = 1 (2011-2010) and Q(t) = 6.03

Substituting this into the equation, we have;

`\begin{gathered} 6.03=a(1)^2\text{ + b(1) + 5.39} \\ \\ 6.03\text{ = a + b + 5.39} \\ \\ a\text{ + b = }6.03\text{ - 5.39 } \\ \\ a\text{ + b = 0.64 } \end{gathered}`

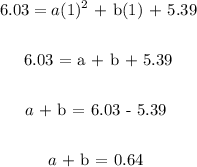
We can have another equation for 2012

For 2012, t = 2 and Q(t) = 6.61

Substituting this into the equation, we have;

`\begin{gathered} 6.61=a(2)^2\text{ + b(2) + 5.39} \\ \\ 6.61\text{ = 4(a) + 2b + 5.39} \\ \\ 4a\text{ + 2b = 6.61 - 5.39} \\ \\ 4a\text{ + 2b = 1.22} \end{gathered}`

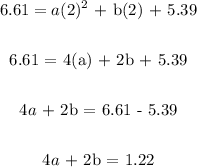
To get the values of a and b, we can proceed to solve the two equations above simultaneously;

a + b = 0.64 ....................(i)

4a + 2b = 1.22 ......................(ii)

We can write the second equation as follows;

2a + 2a + 2b = 1.22

2a + 2(a + b) = 1.22 ..........................(iii)

Kindly recall that a + b = 0.64

Now insert this into equation iii

2a + 2(0.64) = 1.22

2a + 1.28 = 1.22

2a = 1.22 - 1.28

2a = -0.06

a = -0.06/2

a = -0.03

Recall; a + b = 0.64

Hence;

-0.03 + b = 0.64

b = 0.64 + 0.03

b = 0.67

Thus, the quadratic equation is;

`Q(t)=-0.03t^2\text{ + 0.67t + 5.39}`