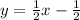Given:
Points on the line (5,2) and (-3,-2)
The slope-interept form of an equation is written as
Solve first for the slope

Now that we have solved for the slope, use any of the two points to solve for the y-intercept. For this case, we will use (5,2) but using (-3,-2) will work just as well.
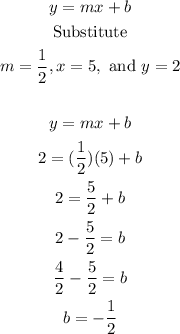
Putting it together, with m = 1/2 and b = -1/2, the equation of the line is