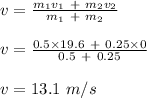Answer:
The velocity of the center of mass of the two-ball system is 13.1 m/s.
Step-by-step explanation:
Given;
mass of the first ball, m₁ = 0.5 kg
mass of the second ball, m₂ = 0.25 kg
initial velocity of the second ball, u₂ = 19.6 m/s
At the highest point the velocity of the second ball, v₂ = 0
The highest point reached by the second ball is calculated as;
v₂² = u₂² - 2gh
0 = u₂² - 2gh
2gh = u₂²
h = u₂² / 2g
h = (19.6²) / (2 x 9.8)
h = 19.6 m
The final velocity of the first ball when it had traveled 19.6 m down;
v₁² = u₁² + 2gh
v₁² = 0 + 2gh
v₁ = √2gh
v₁ = √(2 x 9.8 x 19.6)
v₁ = 19.6 m/s
The velocity of the center of mass of the two-ball system is calculated as;