Question

Consider the density curve plotted below:1920212223240.0250.050.0750.10.1250.150.1750.20.2250.250.275XPDF(X)Density CurveFind P(X≤22) : 0.1Find P(X>21) : Calculate the following. Q1: median: Q3: IQR:

Answer 1

Step-by-step explanation

In this problem, we have a graph of the PDF (Probability Density Function). To compute probabilities in a certain interval (a, b), we must integrate this function from x = a to x = b.

(1) P(X ≤ 22)

We integrate the function from x = -∞ to x = 22, we get:

`\begin{gathered} P(X\text{ }≤\text{ }22)=\int_(-\infty)^(22)dx\cdot PDF(x) \\ =\int_(-\infty)^(20)dx\cdot PDF(x)+\int_(20)^(22)dx\cdot PDF(x) \\ =\int_(-\infty)^(20)dx\cdot0+\int_(20)^(22)dx\cdot0.25 \\ =0+0.25\cdot(22-20) \\ =0.25\cdot2 \\ =0.5. \end{gathered}`

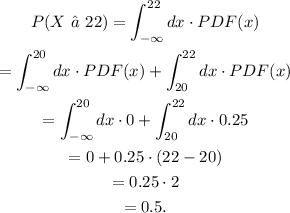
We separated the integral to use the data from the graph.

(2) P(X > 21)

We integrate the function from x = 21 to x = ∞, we get:

`\begin{gathered} P(X>21)=\int_(21)^(\infty)dx\cdot PDF(x) \\ =\int_(21)^(24)dx\cdot PDF(x)+\int_(24)^(\infty)dx\cdot PDF(x) \\ =\int_(21)^(24)dx\cdot0.25+\int_(24)^(\infty)dx\cdot0 \\ =0.25\cdot(24-21)+0 \\ =0.25\cdot3 \\ =0.75. \end{gathered}`

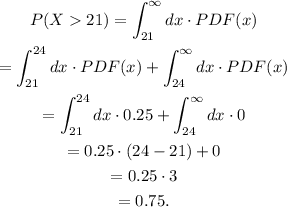
(3) The Q1 is the value x = a of the interval (-∞, a) that gives a probability equal to 0.25. So we must find x such that:

`P(XUsing the data of the graph, we have:[tex]\begin{gathered} \int_(-\infty)^adx\cdot PDF(x)+\int_(20)^adx\cdot PDF(x)=0.25, \\ \int_(-\infty)^(20)dx\cdot0+\int_(20)^adx\cdot0.25=0.25, \\ 0.25\cdot(a-20)=0.25, \\ a-20=(0.25)/(0.25), \\ a-20=1, \\ a=21. \end{gathered}`

(4) The median is the value x = a of the interval (-∞, a) that gives a probability equal to 0.5. Proceeding as before, we have:

`\begin{gathered} \int_(-\infty)^adx\cdot PDF(x)+\int_(20)^adx\cdot PDF(x)=0.5, \\ \int_(-\infty)^(20)dx\cdot0+\int_(20)^adx\cdot0.25=0.5, \\ 0.25\cdot(a-20)=0.5, \\ a-20=(0.5)/(0.25), \\ a-20=2, \\ a=22. \end{gathered}`

(5) The Q3 is the value x = a of the interval (-∞, a) that gives a probability equal to 0.75. Proceeding as before, we have:

`\begin{gathered} \int_(-\infty)^adx\cdot PDF(x)+\int_(20)^adx\cdot PDF(x)=0.75, \\ \int_(-\infty)^(20)dx\cdot0+\int_(20)^adx\cdot0.25=0.75, \\ 0.25\cdot(a-20)=0.75, \\ a-20=(0.75)/(0.25), \\ a-20=3, \\ a=23. \end{gathered}`

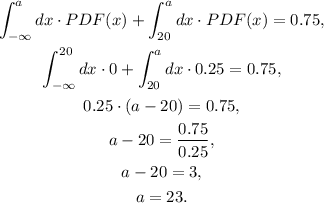
(6) The IQR is given by the difference between Q3 and Q1. Using the results from above, we get:

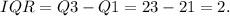
`IQR=Q3-Q1=23-21=2.`Answer

• P(X ≤ 22) = 0.5

,

• P(X > 21) = 0.75

,

• Q1 = 21

,

• median = 22

,

• Q3 = 23

,

• IQR = 2