Question

a.Use the Factor Theorem to find all the zeros of f(x) = x^3 - 8x^2 +17x - 10 given that (x - 2) is a factor. Enter allthe zeros as a comma separated list.Zeros:help (numbers)

Answer 1

The Solution:

Given the polynomial below:

`f(x)=x^3-8x^2+17x-10`

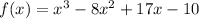
It is given that (x - 2) is a factor of f(x).

We are required to find all the zeros of f(x) using the Factor Theorem.

Step 1:

Recall:

The Factor Theorem states that:

If we divide a polynomial f(x) by (x - c), and (x - c) is a factor of the polynomial f(x), then the remainder of that division is simply equal to 0.

So, we shall divide f(x) by (x - 2), and equate the result to zero.

`\begin{gathered} \text{ x}^2-6x+5 \\ (x-2)\sqrt[]{x^3-8x^2+17x-10} \\ \text{ -(x}^3-2x^2) \\ ---------------- \\ \text{ -6x}^2+17x-10 \\ \text{-(-6x}^2+12x) \\ ---------------- \\ \text{ +5x-10} \\ \text{ -(}5x-10) \\ ----------------- \\ \text{ 0} \end{gathered}`

It follows by the Factor Theorem that:

`x^2-6x+5=0`

Solving the above quadratic equation by the Factorization Method, we get

`\begin{gathered} x^2-5x-x+5=0_{} \\ x(x-5)-1(x-5)=0 \\ (x-1)(x-5)=0 \end{gathered}`

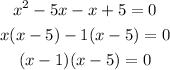
So, we have that:

`\begin{gathered} (x-1)\text{ is a factor of f(x)} \\ x-1=0 \\ x=1 \\ \text{ Thus, 1 is a zero of f(x)} \end{gathered}`

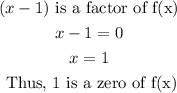
Similarly,

`\begin{gathered} (x-5)\text{ is a factor of f(x)} \\ \text{This means that} \\ x-5=0 \\ x=5 \\ \text{ Thus, 5 is a zero of f(x)} \end{gathered}`

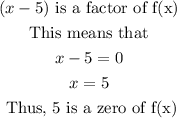
So, the zeros of f(x) are: 2,1,5

Therefore, the correct answers are:

`2,1,5`