Question

does a system of linear equation shown Below have one solution no solution or many solution explain x - 12y = -4x - 9y = 7

Answer 1

to determine wether the system has one solution, an infinite number of solutions or no solution at all we have to solve it.

We have the system:

`\begin{gathered} x-12y=-4 \\ x-9y=7 \end{gathered}`

Substracting the second equation from the first one we have:

`\begin{gathered} (x-12y)-(x-9y)=-4-7 \\ x-12y-x+9y=-11 \\ -3y=-11 \\ y=(11)/(3) \end{gathered}`

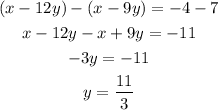
Since we can find a value for the variable y we conclude that the system has only one solution.

The value of x can be found from the first equation once we have y:

`\begin{gathered} x-12((11)/(3))=-4 \\ x-44=-4 \\ x=44-4 \\ x=40 \end{gathered}`

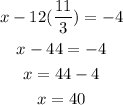
The solution of the sytem is x=40 and y=11/3.