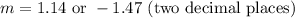Given the quadratic equation below
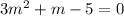
To find m in the form
![m=\frac{N\pm\sqrt[]{D}}{M}](https://img.qammunity.org/2023/formulas/mathematics/college/ey63560hqqurujg3t84gb82x93dsfqf52t.png)
Using the quadratic formula
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{Where x}=m \\ m=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6wumkf5qgqeplqbbipu1qyv1lpctv3t95c.png)
The general form of a quadratic equation is
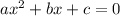
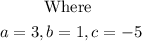
Substitute for a, b and c into the quadratic formula above
![\begin{gathered} m=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ m=\frac{-1\pm\sqrt[]{(1)^2-4(3)(-5)}}{2(3)} \\ m=\frac{-1\pm\sqrt[]{1-(-60)}}{6} \\ m=\frac{-1\pm\sqrt[]{1+60}}{6} \\ m=\frac{-1\pm\sqrt[]{61}}{6} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9xfrjivsifnpqrm0wbqlgt973tw6r9wabs.png)
Hence,
![m=\frac{-1\pm\sqrt[]{61}}{6}](https://img.qammunity.org/2023/formulas/mathematics/college/wsf9ly38bphj87zqphxhxljwzlchk7dczx.png)
The values of N, D and M are
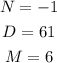
The values of m are
![\begin{gathered} m=\frac{-1+\sqrt[]{61}}{6}=1.13504=1.14\text{ (two decimal places)} \\ m=\frac{-1-\sqrt[]{61}}{6}=-1.46837=-1.47\text{ (two decimal places)} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9qi7c65md7bd80z5uwair2oybh5q5tcqho.png)
Hence, the values of m in two decimal places is