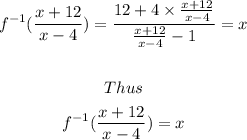Step-by-step explanation
We are to first find the inverse of the function:
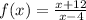
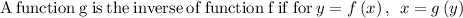
To do so, we will follow the steps below:
Step 1:
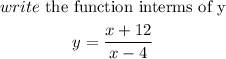
Step2: Interchange x with y
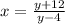
Step 3: solve for y
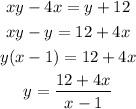
Thus, the inverse of the function is
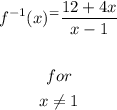
Part 2
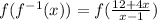
Simplifying further
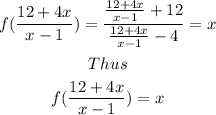
Also
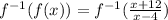
Simplifying further