Question

Find the standard equation of a parabola that has a vertical axis and satisfies the given conditions. vertex (4, −6), x-intercept −3

Answer 1

Given: A parabola that has a vertical axis, vertex (4,-6), and x-intercept of -3.

Required: To find the standard equation of a parabola.

Step-by-step explanation: The equation of the parabola with vertex (h,k) and opening up (a>0) or down (a<0) is

`y=a(x-h)^2+k`

Putting (h,k)=(4,-6) we get

`y=a(x-4)^2+(-6)`

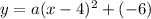
Now, the x-intercept is the point where the curve intersects the x-axis.

Hence, P(x,y)=(-3,0). Putting this in the equation of the parabola and solving for 'a' we get,

`\begin{gathered} 0=a(-3-4)^2-6 \\ a=(6)/(49) \end{gathered}`

Hence the equation of the parabola is

`y=(6)/(49)(x-4)^2-6`

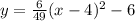
This is the vertex form of the parabola. The standard form of the parabola is

`\begin{gathered} y=(6)/(49)x^2-(48)/(49)x-(198)/(49) \\ \end{gathered}`

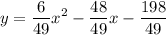
Final Answer: The standard form of the parabola is

`y=(6)/(49)x^2-(48)/(49)x-(198)/(49)`