In this session, we will focus on plotting the function
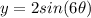
and also finding its amplitude and its period.
To do so, we will use the following:
- the sine function has a period of 2pi.
Given the function of the form
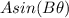
its amplitude would be A and its period would be given by the expression
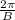
so if we compare this general expression to the function we are given, we can see right away that A=2 and that B=6, since
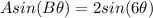
this means that the amplitude of the given function is 2 and the period would be
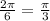
(the period would be pi/3)
To plot this function, we will first recall how the plot of sin(theta) looks like.
From the picture, we can see that there are 4 relevant angles: 0, pi/2, pi, 3pi/2 and 2pi. So the graph of this new function would be exactly the same. The only thing that changes is the scale on the x axis. We will first find the equivalent of this 4 points in the new scale. So we want to solve the following equations
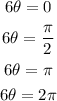
We can find the values by simply dividing both sides by 6. So we get
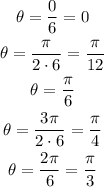
Also, note that the amplitude is 2, so instead of going up until 1 (or down until -1) we go until 2 (or -2). So the new graph looks like this