Question

How do I get to the answer of this question?

Answer 1

To answer this question we will use that alternate interior angles ( for parallel lines) are congruent and that the interior angles of a triangle add up to 180 degrees.

Using the fact that the interior angles of a triangle add up to 180 degrees, we can set the following equation:

`\measuredangle10+\measuredangle9+\measuredangle6=180^(\circ).`

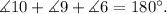
Now, since a||b and angles 9 and 1 are alternate interior angles then:

`\measuredangle9\cong\measuredangle1,`

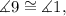
Therefore:

`\measuredangle9=9x-20.`

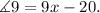
Substituting

`\begin{gathered} \measuredangle9=9x-20, \\ \measuredangle6=2x+6, \\ \measuredangle10=5x-10, \end{gathered}`

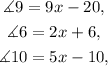
in the first equation we get:

`9x-20+2x+6+5x-10=180.`

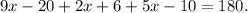
Solving for x we get:

`\begin{gathered} 16x-24=180, \\ 16x=204, \\ x=12.75. \end{gathered}`

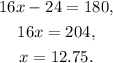
Answer: Option C.