Question

A 171 mL flask contains argon at 1.5 atm and68°C. What amount of Ar is present?Answer in units of mol.R = 0.08206 L.atm/K.mol

Answer 1

Answer: there are 0.0092 moles of argon gas in the flask at the conditions given

Step-by-step explanation:

The question requires us to determine the number of moles of argon gas, given the information provided:

Volume of flask = V = 171 mL

Pressure of gas = P = 1.5 atm

Temperature of gas = T = 68°C

Gas constant = R = 0.08206 L.atm/K.mol

To solve this problem, we can apply the equation for ideal gases, as it follows:

`P* V=n* R* T`

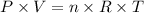
where P corresponds to the pressure of the gas, V is the volume, n is the number of moles, R is the gas constant and T is the temperature.

Note that we are using R in units of L.atm/K.mol, thus the volume must be given in L, the pressure in atm and the temperature in K.

First, we need to convert the volume given from mL to L:

`V=171mL*(1L)/(1000mL)=0.171L`

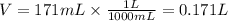
Next, we need to convert the temperature given from °C to K:

`\begin{gathered} T(K)=T(°C)+273.15 \\ T=68°C+273.15=341.15K \end{gathered}`

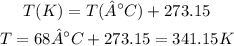
Now that we have volume (0.171 L), pressure (1.5 atm) and temperature (341.15K) in the appropriate units, we can apply these values to the equation of ideal gases and determine the number of moles of gas:

`\begin{gathered} P* V=n* R* T\rightarrow n=(P* V)/(R* T) \\ \\ n=((1.5atm)*(0.171L))/((0.08206L.atm/K.mol)*(341.15K))=0.0092mol \end{gathered}`

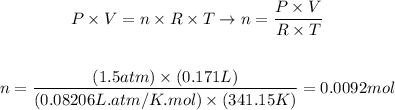
Therefore, there are 0.0092 moles of argon gas in the flask at the conditions given.