Given that the sample contains 6 students, so the sample size will be,
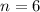
Let the success of the experiment is defined as the event that a randomly selected adult uses a smartphone in meetings or classes. And 'x' be the random variable representing the number of successes.
Given that 58% of the adults use a smartphone in meetings and classes. So there will be 58% chance that a randomly selected adult uses a smartphone in meetings and classes.
So, the probability of success will be,
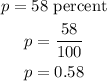
Then, the probability of getting exactly 'x' successes, is given by,
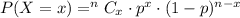
So, the probability of exactly 3 successes will be,
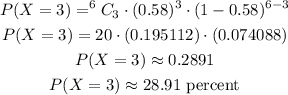
Thus, there is 28.91% probability that exactly 3 of them use their smartphones in meetings or classes.