Item b.)
To solve that item we must remember the general formula for exponential decay, it's
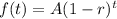
Then, let's modify it to fit our parameters
A is the initial value, in our case, the initial value is the dosage, 500mg, then A = 500
r is the rate, we have 5.2%, then the value of r will be 0.052
And f(t) will transform into D, changing the name.
Hence
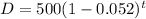
We can also simplify the subtraction, we get
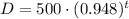
Item c.)
To solve that we will use our equation, we will input t = 6 hours and find the value of D.
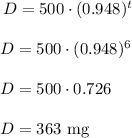
The answer is 363 mg