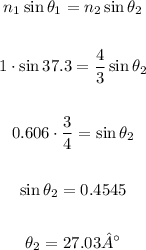Question

A beam of light in air strikes the side of an aquarium at an angle of incidence of 37.3 degrees. The aquarium is made of glass with an index of refraction of 1.59.a. At what angle does the beam enter the glass?b. At what angle does the beam enter the water inside the aquarium?c. At what angle would the beam enter the water if it entered the water directly from the air, without going through the glass?

Answer 1

a.

In order to calculate the angle that the beam enters the glass, let's use the law of refraction.

The index of refraction of the air is 1.

`\begin{gathered} n_1\sin\theta_1=n_2\sin\theta_2\\ \\ 1\sin37.3°=1.59\sin\theta_2\\ \\ 0.606=1.59\sin\theta_2\\ \\ \sin\theta_2=(0.606)/(1.59)\\ \\ \sin\theta_2=0.38113\\ \\ \theta_2=22.4° \end{gathered}`

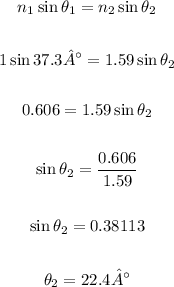
b.

The index of refraction of the water is 4/3, so we have:

`\begin{gathered} n_1\sin\theta_1=n_2\sin\theta_2\\ \\ 1.59\sin22.4=(4)/(3)\sin\theta_2\\ \\ 1.59\cdot0.38113\cdot(3)/(4)=\sin\theta_2\\ \\ \sin\theta_2=0.4545\\ \\ \theta_2=27.03° \end{gathered}`

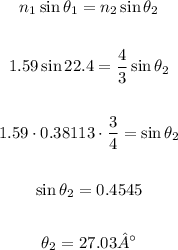
c.

Using the law of refraction from the air to the water, we have:

`\begin{gathered} n_1\sin\theta_1=n_2\sin\theta_2\\ \\ 1\cdot\sin37.3=(4)/(3)\sin\theta_2\\ \\ 0.606\cdot(3)/(4)=\sin\theta_2\\ \\ \sin\theta_2=0.4545\\ \\ \theta_2=27.03° \end{gathered}`