1 Answer

Mogoli · Answer 1 · 2023-05-16T18:05:25+0000

We interpret the question as follows:

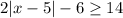
$2|x-5|-6\ge14$

To answer this inequality, we can proceed as follows:

1. Add 6 to both sides of the inequality:

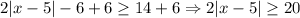
$2|x-5|-6+6\ge14+6\Rightarrow2|x-5|\ge20$

2. Divide both sides of the inequality by 2:

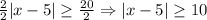
$(2)/(2)|x-5|\ge(20)/(2)\Rightarrow|x-5|\ge10$

Then, using a property of inequalities when is present the absolute value function, we have:

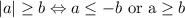
$|a|\ge b\Leftrightarrow a\leq-b\text{ or a}\ge b$

Now, we can apply it as follows:

$x-5\leq-10\text{ or x-5}\ge10$

And we have to solve both inequalities separately as follows:

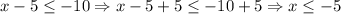
$x-5\leq-10\Rightarrow x-5+5\leq-10+5\Rightarrow x\leq-5$

And

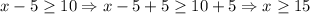
$x-5\ge10\Rightarrow x-5+5\ge10+5\Rightarrow x\ge15$

We can graph both solutions as follows:

We can see that above the numbers, we have either a [ or ], or a solid point to represent that the number is included in the solution.

In summary, therefore, the solution for the inequality above is:

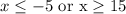
$x\leq-5\text{ or x}\ge15$

We can also represent this solution in interval form as follows:

$(-\infty,-5\rbrack\cup\lbrack15,\infty)$

Please log in or register to add a comment.