Question

Vector A has a magnitude of 50units and points in the positive x direction. A second vector B has a magnitude of 120 units and points at an angle of 70 degree below the x axis. which vector has (a) the greater x component. and (b) the greater y component.

Answer 1

A has the greater x component

B has teh greater y component

Step-by-step explanation

Step 1

find the components x and y for each vector

so

for A)

`\begin{gathered} \lvert A\rvert=50 \\ \text{direction = 0\degree to x positive} \\ \text{henc} \\ A_x=\lvert A\rvert\cos \theta \\ A_x=50\cdot\cos \text{ 0} \\ A_x=50\cdot1 \\ A_x=50 \\ \text{Now, the y-component} \\ A_y=\lvert A\rvert\sin \theta \\ A_y=50\sin 0 \\ A_y=50\cdot0 \\ A_y=0 \end{gathered}`

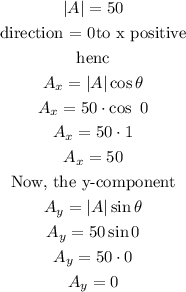
hence,

A( component x=50

A(component y=0)

Now, for

B)

`\begin{gathered} \lvert B\rvert=120 \\ \theta=-70 \\ \text{hence} \\ B_x=120\cdot\cos (-70) \\ B_x=41.04 \\ \text{and the y-component} \\ B_y=50\cdot\sin (-70) \\ B_y=50\cdot\sin (-70) \\ B_y=-46.98 \end{gathered}`

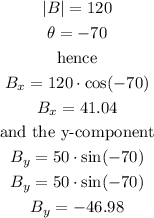
Step 2

compare

a)which vector has (a) the greater x component

`\begin{gathered} A_x=50 \\ B_x=41.014 \\ 50>41.04,\text{hence} \\ A_x>B_x \\ \text{the vector A has the greater x component } \end{gathered}`

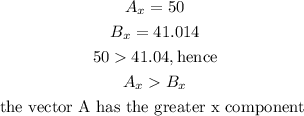
(b) the greater y component.​

`\begin{gathered} A_y=0 \\ B_y_{}=-49.68 \\ \end{gathered}`

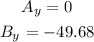
the negative sign in the y-component of B means, it is below the x -axis, but the component ( length) is greater than zero, so

B has athe greater y component

x