Question

5. Is the line whose equation is y=-x+3 tangent to the circle whose equation is (x+5)*+(y – 5) = 16? Justify your answer algebraically and graphically.

Answer 1

Equation of line y=-x+3

equation of circle : (x+5)^2 + (y-5)^2=16

To proove that the equation of line is the tangent to circle,

Find the gradient of the radius of the circle (n) and the slope of the given line (m)

if mn=-1,

the the line is tangent to the circle

Slope of Line :

Equation of line y= -x+3

Slope of the line is m=-1

Gradient of radius of circle :

consider any coordinates of the circle,

`\begin{gathered} (x+5)^2+(y-5)^2=16 \\ at\text{ x=0} \\ (0+_{}5)^2+(y-5)^2=16 \\ 25+(y-5)^2=16 \\ (y-5)^2=16-25 \\ (y-5)^2=9 \\ y-5=9 \\ y=14 \\ So,\text{ the coordinates of circel are : (0,14)} \end{gathered}`

Since the radius of circle is : (-5, 5)

Gardient of radius of circle is expressed as :

`\begin{gathered} \text{Gradient = }(y_2-y_1)/(x_2-x_1) \\ \text{Gradient}=(14-5)/(0-(-5)) \\ \text{Gradient (n)=}(9)/(5) \end{gathered}`

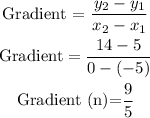
so the product of n and m is

`\begin{gathered} n* m=(9)/(5)*(-1) \\ n* m=-(9)/(5) \\ n* m\\e(-1) \end{gathered}`

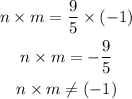
So, the given equation of line is tangent to the circle,

In the graph it clearly show that the line is passes through the circle, it does not touch the circle at a single point,

So the line y=-x+3 is not the tangent to the circle (x+5)^2+(y-5)^2 =16