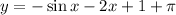Question

Find the particular solution to y "= sin(x) given the general solution y = -sin(x) + Ax + B and the initial conditions

Answer 1

Given:

Given the differential equation

`y^(\prime)^(\prime)=\sin x`

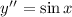
having the general solution y = -sin x + Ax + B.

Required: Particular solution satisfying the initial conditions

`y((\pi)/(2))=0\text{ and }y^(\prime)((\pi)/(2))=-2`

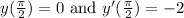
Step-by-step explanation:

Plug the first initial condition to the general solution.

`\begin{gathered} 0=-\sin((\pi)/(2))+A\cdot(\pi)/(2)+B \\ A\cdot(\pi)/(2)+B=1\text{ ... \lparen1\rparen} \end{gathered}`

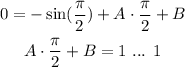
Now, find the derivative of the general solution.

`y^(\prime)(x)=-\cos x+A`

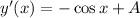
Plug the second initial condition.

`\begin{gathered} -2=-\cos((\pi)/(2))+A \\ A=-2 \end{gathered}`

Substitute the value of A in equation (1).

`\begin{gathered} -2\cdot(\pi)/(2)+B=1 \\ B=1+\pi \end{gathered}`

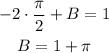
Now, substitute the values of both A and B into the general solution of the differential equation.

`y=-\sin x-2x+1+\pi`

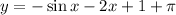
Final Answer: The particular solution is

`y=-\sin x-2x+1+\pi`