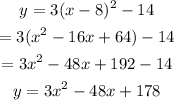Question

What's the equation of the parabola that has it's vertex at (8,-14) and contains the point ( 5,13)?

Answer 1

The equation of the parabola is:

`y=3x^2-48x+178`

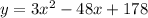
Step-by-step explanation:

The equation of a parabola is written as:

`y=a(x-h)^2+k`

Where h and k are coordinates of the vertex of the parabola, and x and y are the coordinates of the point.

h = 8, k = -14, x = 5, y = 13

Substituting these values into the equation, we have

`13=a(5-8)^2+(-14)`

Solving this, we will have the value for a.

`\begin{gathered} 13=a(-3)^2-14 \\ \text{Add 14 to both sides} \\ 13+14=a(-3)^2-14+14 \\ 27=a(-3)^2 \\ 27=9a \\ \text{Divide both sides by 9} \\ a=(27)/(9)=3 \end{gathered}`

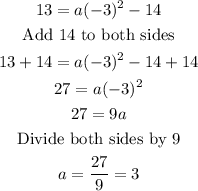
Using this value of a, the equation becomes

`\begin{gathered} y=3(x-8)^2-14 \\ =3(x^2-16x+64)-14 \\ =3x^2-48x+192-14 \\ y=3x^2-48x+178 \end{gathered}`