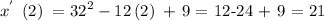Question

Find the open t-intervals on which the particle is moving to the right. (Enter your answer using interval notation.)

Answer 1

`21\text{ m/s}`

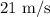
Step-by-step explanation:

Here, we want to get the velocity of the particle when the acceleration is zero

From the question, we have to differentiate twice to get the acceleration:

Now, let us get the value of t wt which acceleration is zero:

`\begin{gathered} Given\text{ x\lparen t\rparen} \\ x^(\prime)^\left(t\right)\text{ = 3t}^2-12t\text{ +}9 \\ x^(\prime)^(\prime)\left(t\right)\text{ = 6t-12} \end{gathered}`

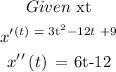
Now, let us calculate the t value when the second differential is zero

Mathematically, we have that as:

`\begin{gathered} 6t-12\text{ = 0} \\ 6t\text{ = 12} \\ t\text{ = }(12)/(6) \\ t\text{ = 2 secs} \end{gathered}`

What this simply means is that the acceleration is zero when t = 2

Now, let us get the velocity when t = 2

We simply substitute the value of t into the first differential

Mathematically, we have that as:

`x^{^(\prime)\text{ }}\left(2\right)\text{ = 3\lparen2\rparen}^2-12\left(2\right)\text{ + 9 = 12-24 + 9 = 21 }`