Given:
mean, μ = 165
Standard deviation, σ = 13
n = 150
Let's find how many of them she would expect to score less than 149.
Apply the z-score formula:

Thus, we have the z-score:
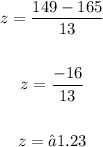
Here, we are to solve for: P(x < 149).
We have:
P(x < 149) = P(z < -1.23)
Using the standard normal table, we have:
NORMSDIST(-1.23) = 0.10935
Therefore, out of the 150 games, the expected score less than 149 would be:
150 x 0.10934 = 16.4 ≈ 16
The expected number to score le