To answer this question we will set y=0 and then solve for x.
Setting y=0 we get:
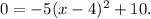
Adding 5(x-4)² to the above result we get:
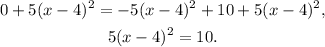
Dividing the above result by 5 we get:
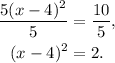
Therefore:
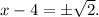
Adding 4 to the above result we get:
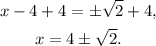
Since y represents the daily profit in hundreds of dollars, then the zeros are where the daily profit is $0.00.
Answer: Options A and B.