Question

expansion1x ftoriginal garden(x+4) ft —-7 ft →a. Write binomials that represent the length and width of the enlarged garden.b. In the enlarged garden, how many feet longer is the length than the width?c. The area of the enlarged garden is 266 square feet. Find the dimensions of the original garden and theenlarged garden.2. A moving company supplies packing boxes for its customers. The dimensions of the

Answer 1

Given the area is,

`x^2+17x+66`

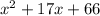
this can be written as,

`(x+11)(x+6)`

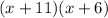
that means one dimension had increased by 11 and the other by 6. So calculating the area. first we can set the area of the emlarged garden to be 266 feet

Thus,

`\begin{gathered} (x+11)(x+6)=266 \\ x^2+17x+66=266 \end{gathered}`

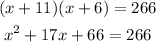
To solve the above equation, let us subtract 266 from each side,

`\begin{gathered} x^2+17x-200=0 \\ (x-8)(x+25)=0 \\ x=8;x=-25 \end{gathered}`

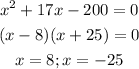
ignoring the negative value, x=8, that is the original dimension is 8 feet each

so the enlarged values are,

length= x+11=8+11=19 feet

width = x+6=8+6=14 feet

Thus the length is 5 feet more than width in the enlarged garden