Answer:
Desktop = $2400
Laptop = $2200
Explanation;
The formula for the interest is:
![I=P[(1+r)^t-1]](https://img.qammunity.org/2023/formulas/mathematics/college/4ldix1wr4l99490f7ktzp8eunjwhwzfe1u.png)
Where:
• I is the interest after t years
,
• r is the rate of compounding, in decimal
,
• t is the years of compounding
In this case, let's call L = price of the laptop, D = price of the desktop
Since the laptop costs $200 less than the desktop:
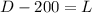
Also, if we call I_D = interest of the desktop and I_L interest of the laptop, we know that the total after one year is

Now, we can write the equations for both financing plans:
![\begin{gathered} I_D=D[(1+0.08)^t-1] \\ I_L=L[(1+0.065)^t-1] \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/oythylpwe44tri0q3or0f6o9mzehsi4rfx.png)
So far we have:
![\begin{gathered} (1)\text{ }D-200=L \\ (2)\text{ }I_D+I_L=335 \\ (3)I_D=D[(1+0.08)^t-1] \\ (4)\text{ }I_L=L[(1+0.065)^t-1] \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lgjuearups6dd9t9fhyszzgxvtbrk01u4n.png)
Now, we can write:
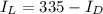
And replace in the equation (4):
![335-I_D=(D-200)[1.065^t-1]](https://img.qammunity.org/2023/formulas/mathematics/college/ri21i66c9sv031hcp8q6i23koin86qzzzt.png)
Since t = 1 (one year passed)
we can solve for I_D:
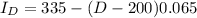
And solve:
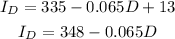
Now, we can equate this with equation (3):
![\begin{cases}I_D=348-0.065D{} \\ I_D=D[(1+0.08)^t-1]\end{cases}](https://img.qammunity.org/2023/formulas/mathematics/college/zhncxg3l0mo2pdq3gc94bk4gt3zjtdc12t.png)
But, before, let's make some work on the equation 3. Snce t = 1:
![\begin{gathered} I_D=D[(1+0.08)^1-1] \\ I_D=0.08D \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wrkldwy1feg98p2mrfjg7a7kcr92owcfao.png)
Now equate:
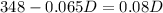
And solve for D:
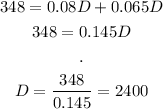
The price of the desktop computer is $2400. Now we can find the price of the laptop using the equation (1):
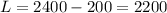
The price of the laptop is $2200