Question

Graph:-(x²+y²-1)³ = x^2y³.

Answer 1

Graph:

`\left(x^2+y^2-1\right)^3=x^2y^3`

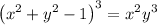
If we replace x with -x, we get the very same expression. This means the function is even, i.e., it's symmetric with respect to the y-axis.

We only have to use values of x greater or equal to 0 and reflect the graph over the y-axis.

For x = 0:

`\left(y^2-1\right)^3=0`

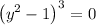
We get y = 1 and y = -1

For x = 1:

`\begin{gathered} \left(y^2\right)^3=y^3 \\ \\ Or: \\ \\ y^6=y^3 \end{gathered}`

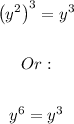
Which gives y = 0, y = 1

For x = 0.5

`\left(y^2-0.75\right)^3=0.25y^3`

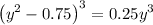
Which gives y = 1.24 and y = -0.6

You can add more points as desired and have a better graph.

Below is the graph: