If there's an inverse variation between x and y then the relation between them can be represented by:
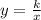
Where k is a constant. Let's see if the table represents an inverse variation. We can start with the first column x=1 and y=60:
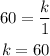
So according to the first column the relation is:
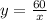
Let's see if the rest of the table agrees with this. We can take x=2,3,4,5 and 6 and see if the values of y are the same as those in the table:
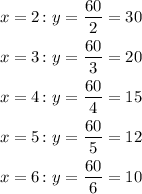
So the y-values given by y=k/x are the ones displays in the table. Then the table represents an inverse variation.