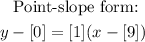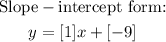Given the linear equation;

Note that the slope of a line perpendicular to another has its slope as a negative inverse of the first one.
This means if the slope of line 1 is m, then the slope of a perpendicular line which is line 2 would be the negative inverse of m, that is;
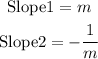
The slope of the line given is -1. The slope is the coefficient of x.
For a line perpendicular to this one;
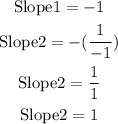
The slope of the perpendicular line is 1, and we already have a point along this line given as
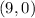
The equation of a line in point-slope form is;

Where the variables are;
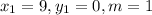
The equation in point-slope form now becomes;

For the equation in slope-intercept form, the general form of the equation is;

Here also the variables are;
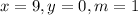
Substituting the variables we now have;

The equation now would be re-written as;
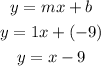
ANSWER: