Question

A nickel (Ni #28) (density 8.90 g/ml) cube has each side equal to 23.00 mm. How many grams does it weigh?

Answer 1

The mass of nickel is 108.29 grams

Explanation:

Given data

The density of nickel = 8.90 g/mL

The nickel has a cube shape and each of the sides has a length of 23.00mm

Let x represent the mass of nickel in grams

Recall that

`\begin{gathered} \text{Volume }ofacube=a^3 \\ where\text{ a = 23.00}mm^{} \\ \text{volume = (23.00)}^3 \\ \text{volume of a cube = 12167 mm}^{3^{}} \end{gathered}`

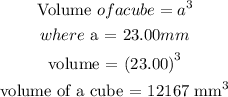
The next step is to convert the cubic millimeter to milliliter

According to the Standard International Unit, 1 mm^3 = 0.001 mL

`\begin{gathered} 1\text{ }\rightarrow\text{ 0.001} \\ 12167\text{ }\rightarrow\text{ x} \\ \text{cross multiply} \\ 1\cdot\text{ x = 0.001 x 12167} \\ x\text{ = }12.167\text{ ml} \end{gathered}`

Therefore, the volume of Nickel is 12.167 mL

We can get the value of mass using the below formula

`\begin{gathered} \text{ Denisty = }\frac{mass}{\text{volume}} \\ 8.90\text{ = }(x)/(12.167) \\ \text{cross multiply} \\ x\text{ = 8.90 x 12.167} \\ x\text{ = 108.29 grams} \end{gathered}`

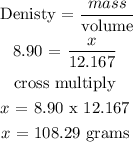
Therefore, the mass of nickel is 108.29 grams