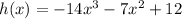Question

Identify the function that reflects f(x)= 14x^3 -7x^2 +6 across the y axis and shifts it 6 units up.

Answer 1

We have the function:

`f(x)=14x^3-7x^2+6.`

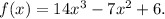
We must identify the function that:

0. reflects the function across the y-axis,

,

1. shift it 6 units up.

1) To reflect the function across the y-axis we replace x by -x:

`f(x)\rightarrow g(x)=14(-x)^3-7(-x)^2+6=-14x^3-7x^2+6.`

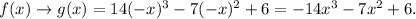
2) To shift the result 6 units up, we sum +6 on the right side:

`g(x)\rightarrow h(x)=-14x^3-7x^2+6+6=-14x^3-7x^2+12.`

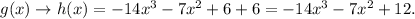
Plotting both functions, we get:

Answer

Second option

`h(x)=-14x^3-7x^2+12`