Question

A ball is thrown upward with a speed of 38.0 m/s from the top of a building 240 m tall.h) suppose the ball was actually thrown downward with a speed of 38.0 m/s, how long will it take the ball to reach the ground? i) if the ball was actually thrown downward with the speed of 38.0 m/s what would be it’s speed when it hit the ground?

Answer 1

Given:

Initial speed = 38.0 m/s

Height of builiding = 240 m

Let's determine the following:

(h) Time it will take the ball to reach the ground suppose the ball was thrown downward with a speed of 38.0 m/s.

To find the time it will take to reach the ground, apply the formula:

`h=ut+(1)/(2)gt^2`

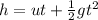
Where:

h = -240 m

u = -38.0 m/s

g is the acceleration due to gravity = 9.8 m/s^2

Thus, we have:

`\begin{gathered} -240=-38t-(1)/(2)\ast9.8t^2 \\ \\ -240=-38t-4.9t^2 \end{gathered}`

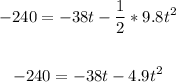
Move all terms to the left and equate to zero:

`4.9t^2+38t-240=0`

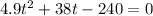
Solve for t using quadratic formula:

`\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where:

a = 4.9

b = 38

c = -240

Thus, we have:

`\begin{gathered} \frac{-38\pm\sqrt[]{38^2-4(4.9)(-240)}}{2(4.9)} \\ \\ \frac{-38\pm\sqrt[]{1444-(-4704)_{}}}{9.8} \\ \\ \frac{-38\pm\sqrt[]{1444+4704_{}}}{9.8} \\ \\ (-38\pm78.409)/(9.8) \\ \\ (38-78.409)/(9.8),(38+78.409)/(9.8) \\ \\ =-11.88,4.12 \end{gathered}`

Let's take the positie value, 4.12.

Therefore, the time it will take the ball to reach the ground is 4.12 seconds.

(i) If the ball was actually thrown downward with the speed of 38.0 m/s what would be it’s speed when it hit the ground?

To find the speed, apply the formula:

`v=u-gt`

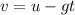
Where:

u = -38.0 m/s (downward speed)

g = 9.8 m/s^2

t = 4.12 seconds

Thus, we have:

`\begin{gathered} v=-38.0-9.8(4.12) \\ \\ v=-38.0-40.376 \\ \\ v=-78.38 \end{gathered}`

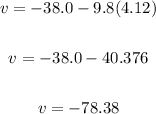
Thereforem the speed is -78.38 m/s.

ANSWER:

(h) 4.12 seconds

(i) -78.38 m/s