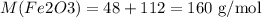Question

Iron is generally produced from iron ore through the following reaction in a blast furnace. If400 g of Fe2O3 are available to react, how many moles of CO are needed?Fe2O3 + 3C0 + 2Fe + 3CO2

Answer 1

Step 1 - Understanding the relation of moles

The reaction between Fe2O3 and CO is:

`Fe_2O_(3(s))+3CO_((g))\rightarrow2Fe_((s))+3CO_(2(g))`

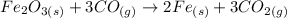
We can see in this equation that 1 mole of Fe2O3 consumes 3 moles of CO. This is a fixed proportion that we'll be using to solve the problem.

Step 2 - Finding how many moles of Fe2O3 have reacted

To discover how many moles (n) of Fe2O3 have reacted, we can divide the mass (400g) by the molar mass of Fe2O3 (159 g/mol):

`n=(m)/(M)=(400)/(159)=2.51\text{ moles}`

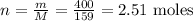
Step 3 - Finding how many moles of CO are needed

Now that we know how many moles of Fe2CO3 reacted, we can set the following proportion:

`\begin{gathered} 1\text{ mole of Fe2O3 consumes --- 3 moles of CO} \\ 2.51\text{ moles of Fe2O3 consume ---- x} \\ \\ x=(3*2.51)/(1)=7.53\text{ moles of CO} \end{gathered}`

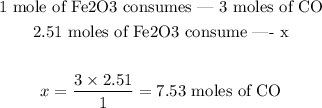
Therefore, 7.53 moles of CO are needed.

Note: Finding the molar mass of Fe2O3

Multiply the molar mass of each element by the number of times it appears in the formula and then sum it all up. The molar masses are 16 g/mol for O and 56 g/mol for Fe. We have thus:

`\begin{gathered} O\rightarrow3*16=48 \\ \\ Fe\rightarrow2*56=112 \end{gathered}`

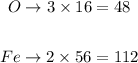
The molar mass will be thus:

`M(Fe2O3)=48+112=160\text{ g/mol}`