This question is about the intersection of functions.
When we say that two functions are equal at a certain value, it means their graph meet at that point.
In this case, we have two functions
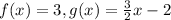
To find the exact value where these functions are equal, we need to make them equal
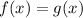
Replacing the functions, we have
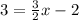
Now, we solve for x
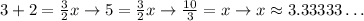
This means the x-value at which the two functions' values are equal is 10/3, or 3.333...
Additionally, the y-value at which the two function's values are equal is 3.
Therefore, these functions are equal at point (10/3 , 3).