Question

An airplane flies at 500 mph with a direction of 135° relative to the air. The plane experiences a wind that blows 60 mph with a direction of 60°.Part A: Write each of the vectors in linear form. Show all necessary calculations. (6 points)Part B: Find the sum of the vectors. Show all necessary calculations. (2 points)Part C: Find the true speed and direction of the airplane. Round the speed to the thousandths place and the direction to the nearest degree. Show all necessary calculations. (7 points)

Answer 1

The diagram above shows the vector for the plane, which is 500 mph at 135 degrees, along with the vector for the wind, which is 60 mph at 60 degrees. One thing that we know about vectors is that we can move them around, so long as we don't change their magnitude or direction, so, we can draw a diagram like this:

We moved the wind vector on top of the plane vector, and the dotted line represents the sum of the two vectors. Lets now look at each vector separately and solve part A:

The one above is the plane vector. To find an equation in linear form, we have to solve for its components using trigonometry. Note that there is a 45 degrees in there because 180 - 135 is 45, and this makes calculations easier. The cosine of 45 degrees is x/500. We can use this to solve for the x component:

`\begin{gathered} cos(45)=(x)/(500) \\ \frac{\sqrt[\placeholder{⬚}]{2}}{2}*500=x \\ x=250\sqrt[\placeholder{⬚}]{2}\approx353.553 \end{gathered}`

Note that x is in the negative direction, so our actual component is -353.55. Let's do the same for the y component, given that sin(45) is y/500:

`\begin{gathered} sin(45)=(y)/(500) \\ \frac{\sqrt[]{2}}{2}*500=y \\ y=250\sqrt[\placeholder{⬚}]{2}\approx353.553 \end{gathered}`

Therefore, our plane vector is -353.553i + 353.553j (i and j are direction vectors)

We can now do the same thing for the wind vector:

Our x component is the following:

`\begin{gathered} cos(60)=(x)/(60) \\ (1)/(2)*60=x \\ x=30 \end{gathered}`

Our y component is the following:

`\begin{gathered} sin(60)=(y)/(60) \\ \frac{\sqrt[]{3}}{2}*60=y \\ y=30\sqrt[\placeholder{⬚}]{3}\approx51.962 \end{gathered}`

Therefore, our wind vector is 30i + 51.962j

For part B, we have to find the sum of the plane and wind vectors. All we have to do for that is add up the i components and add up the j components. The calculation is below:

`\begin{gathered} -353.553i+353.553j+(30i+51.962j)=(-353.553+30)i+(353.553+51.962)j \\ =-323.553i+405.515j \end{gathered}`

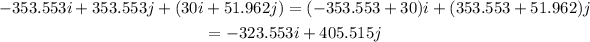
Therefore, the sum of the vectors is -323.553i + 405.515j

For part C, we have to find the magnitude and direction of the new vector that we calculated (the sum of the plane and wind vectors). Below is the graph for the sum of the vectors:

To find r, which is the true speed of the plane we can use the Pythagorean theorem (since the triangle above is a right triangle). The Pythagorean theorem says that the hypotenuse squared is the sum of each of the legs squared. Let's calculate r:

`\begin{gathered} r^2=323.553^2+405.515^2 \\ r^2=104686.544+164442.415 \\ r^2=269128.959 \\ r\approx518.776 \end{gathered}`

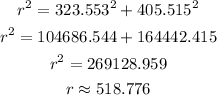
To find theta, which is the direction, we can take use the fact that tangent of theta is opposite over adjacent. Therefore, theta is the inverse tangent of the opposite side (405.515) over the adjacent side (-323.553). The calculation is below:

`\theta=tan^(-1)((405.515)/(-323.553))=tan^(-1)(1.253)=128.593\approx129`

Therefore, the true speed is 518.776 mph and the direction of the airplane is 129 degrees relative to the air

Part A: plane vector is -353.553i + 353.553j, wind vector is 30i + 51.962j

Part B: sum of the vectors is -323.553i + 405.515j

Part C: true speed is 518.776 mph and the direction of the airplane is 129 degrees relative to the air