Given the points:
(x1, y1) = (-12, 1)
(x2, y2) ==> (-8, 6)
To find the slope, use the slope formula below:
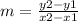
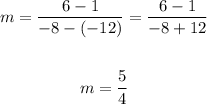
The slope of the line is:
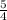
If the order of the points is reversed, let's find the slope.
First swap the order of the points:
(x1, y1) ==> (-8, 6)
(x2, y2) ==> (-12, 1)
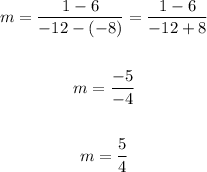
Therefore, if the order of the points is reversed, the slope will still be the same.
ANSWER:
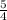
If the order of the points is reversed, the slope will remain the same.