Question

Let f (x)=4x-7. Find the inverse of f. Be sure to write your answer using inverse notation.

Answer 1

Hello there. To solve this question, we have to remember some properties about determining the inverse of a function.

First, a function is called invertible if it is bijective, that is, it is both injective and surjective.

This inverse is unique, in the sense that for a function f(x), there exists only g(x) such that

`g(x)=f^(-1)(x)`

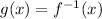
The property that inverse functions satisfy is

`f(f^(-1)(x))=x`

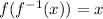
And we'll use it to find it.

Okay. First, suppose that this function has an inverse g(x), that we'll call as

`g(x)=y`

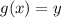
So using the property on inverse functions, we get

`f(y)=4y-7`

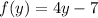
So this might be equal to

`4y-7=x`

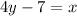
Solve the equation for y.

Add 7 on both sides of the equation

`4y=x+7`

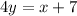
Divide both sides of the equation by a factor of 4

`y=(x)/(4)+(7)/(4)`

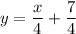
Such that we get

`f^(-1)(x)=(x)/(4)+(7)/(4)`

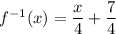
This is the inverse of f.