Hi, can you help me answer this question please, thank you!

Question

asked Jan 7, 2023 103k views

1 Answer

Prashant Bhardwaj · Answer 1 · 2023-01-12T09:14:56+0000

Given:

alpha level = 0.001

Population 1

success = 122

sample size n₁ = 202

Population 2

success = 220

sample size n₂ = 340

Find: test statistic and p-value

Solution:

Based on the given sample, we have two proportions here. Thus, we will be using test of two proportions formula.

$z=\frac{p_1-p_2}{\sqrt[]{p(1-p)((1)/(n_1)+(1)/(n_2))}}$

To be able to use the formula, we need to identify first the value of p, p₁, and p₂.

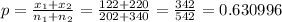
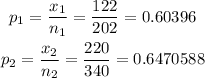
$\begin{gathered} p_1=(x_1)/(n_1)=(122)/(202)=0.60396 \\ p_2=(x_2)/(n_2)=(220)/(340)=0.6470588 \end{gathered}$

We now have the values of p, p₁, and p₂ as well as n₁ and n₂ (sample size).

p = 0.630996

p₁ = 0.60396

p₂ = 0.6470588

n₁ = 202

n₂ = 340

Let's plug this in to the test of two proportions formula above.

$z=\frac{0.60396-0.6470588}{\sqrt[]{0.630996(1-0.630996)((1)/(202)+(1)/(340))}}$

Solve for z.

$z=\frac{-0.0430988}{\sqrt[]{0.23284((271)/(34340))}}=(-0.0430988)/(0.042866)\approx-1.005$

The test-statistic is equal to -1.005.

The p-value equivalent for this is 0.1573.