Question

Light passes from air into water at an angle of 40.0° to the normal. What is the angle of refraction?

Answer 1

Light passes from air into water at an angle of 40.0° to the normal.

The angle of refraction is smaller than the angle of incidence when light passes from a lower density medium (air = 1) to a higher density medium (water = 1.333)

The angle of refraction can be found using Snell's law given by

`n_1\cdot\sin \alpha_1=n_2\cdot\sin \alpha_2`

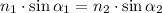
Where

n₁ = Refractive index of the air = 1

n₂ = Refractive index of the water = 1.333

α₁ = Angle of incidence = 40.0°

α₂ = Angle of refraction = ?

Let us substitute these values into the above equation and solve for α₂

`\begin{gathered} n_1\cdot\sin \alpha_1=n_2\cdot\sin \alpha_2 \\ 1_{}\cdot\sin (40.0\degree)_{}=1.333\cdot\sin \alpha_2 \\ \sin \alpha_2=\frac{1_{}\cdot\sin (40.0\degree)_{}}{1.333} \\ \sin \alpha_2=0.4822 \\ \alpha_2=\sin ^(-1)(0.4822) \\ \alpha_2=28.9\degree \end{gathered}`

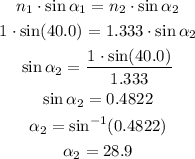
Therefore, the angle of refraction is 28.9°