ANSWER

Step-by-step explanation
First, we have to express the vectors in their component forms.
For the vector with a length of 101 m:
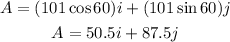
For the vector with a length of 85.0 m:

Hence, the sum of the two vectors is:
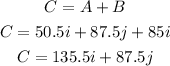
To find the direction of the sum of the vectors, apply the formula:
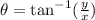
where x = horizontal component of the sum
y = vertical component of the sum
Therefore, the direction of the sum of the vectors is:

That is the answer.