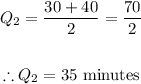a)
The mean waiting time per child can be calculated using the formula:
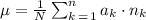
Where a_k is the time, n_k is the number of children for time k, and N is the total number of children. Using the data from the problem:

b)
For the median, we calculate the tentative position of the median using the equation:
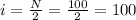
Since this is an integer number, the real median is the semi-sum of the elements at positions i and (i+1). From the table, these elements are 30 and 40, so the median is: