Question

In diagram 2, STUV is a rhombus and RSV is a straight line.Calculate the value of x+yA. 145B. 140C. 135 D. 130

Answer 1

Since STUV is a rhombus,

Therefore,

Adjacent sides of a rhombus are supplementary, that is they add to give 180°

`\angle TSV+\angle UVS=180^0`
`\begin{gathered} \angle TSV=70^0 \\ \angle UVS=2x^0 \end{gathered}`

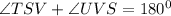
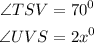
Substituting the values above, we will have

`\begin{gathered} \angle TSV+\angle UVS=180^0 \\ 70^0+2x^0=180^0 \end{gathered}`

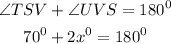
Subtract 70 from both sides,

`\begin{gathered} 70^0+2x^0=180^0 \\ 70-70+2x=180-70 \\ 2x=110 \end{gathered}`

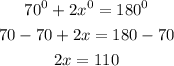
Divide both sides by 2 ,

`\begin{gathered} 2x=110 \\ (2x)/(2)=(110)/(2) \\ x=55^0 \end{gathered}`

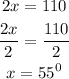
Let's consider the quadrilateral TPUV

The sum of angles in a quadrilateral is

`=360^0`
`\begin{gathered} \angle UPT=90^0 \\ \angle VUP=70^0 \\ \angle UVT=70^0(corresspond\text{ to }\angle VST \\ \angle PTV=w \end{gathered}`
`\angle UPT+\angle VUP+\angle UVT+\angle PTV=360^0`

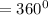
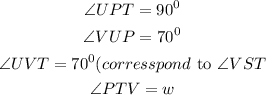
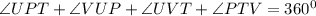
Substituting the values, we will have

`\begin{gathered} 90^0+70^0+70^0+w=360^0 \\ 230^0+w=360^0 \\ \text{substract 230 from both sides} \\ 230^0-230^0+w=360^0-230^0 \\ w=130^0 \end{gathered}`

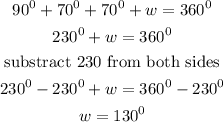
Consider the line PTQ

`\angle PTV+\angle QTV=180(angles\text{ in a straight line)}`
`\begin{gathered} \angle QTV=z \\ \angle PTV=130^0 \end{gathered}`
`\begin{gathered} \angle PTV+\angle QTV=180 \\ 130^0+z=180^0 \\ z=180^0-130^0 \\ z=50^0 \end{gathered}`

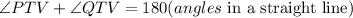
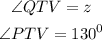
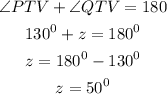
Lastly, let's consider the triangle RTQ

`\angle QRT+\angle QTV+\angle TQR=180^0`
`\begin{gathered} \angle QRT=50^0 \\ \angle QTV=50^0 \\ \angle TQR=y^0 \end{gathered}`

`\begin{gathered} \angle QRT+\angle QTV+\angle TQR=180^0 \\ 50^0+50^0+y^0=180^0 \\ 100+y^0=180^0 \\ y^0=180^0-100^0 \\ y^0=80^0 \end{gathered}`

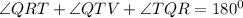
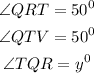
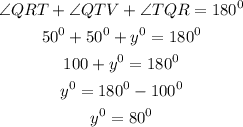
Hence,

The value of x+y will be

`\begin{gathered} x+y \\ =55^0+80^0 \\ =135^0 \end{gathered}`

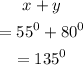
Therefore,

The final answer is OPTION C