The sample space of throwing two dices is shown below:
(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)
(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)
(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)
(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)
(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)
(6,1)(6,2)(6,3)(6,4)(6,5) (6,6)
We know that the probability of an event is given by:
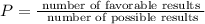
From the sample space above we notice that only three possible results will give either 2 or 11, then we have:
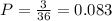
Multiplying by 100 to get the probability in percent form we have 8.3%
Therefore, the probability is 8.3%