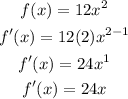Question

Rewriting a Function Before Differentiating, complete the table to find the derivative of the function.

Answer 1

We are given the function:

`y=(3)/((2x)^(-2))`

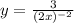
To rewrite this, we need to remember that negative exponents mean the reciprocal of the expression. So we get:

`\begin{gathered} y=(3)/((2x)^(-2)) \\ \\ y=3(2x)^2 \\ \\ y=3(4x^2) \\ \\ y=12x^2 \end{gathered}`

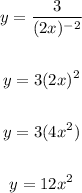
To differentiate, we bring down the exponent as a multiplier, then reduce the original exponent by 1.

`\begin{gathered} y^(\prime)=12(2)x^(2-1) \\ \\ y^(\prime)=24x \end{gathered}`

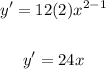
The derivative of f(x) = x^a is f'(x) = ax^(a-1).

`\begin{gathered} f(x)=x^a \\ f^(\prime)(x)=ax^(a-1) \end{gathered}`

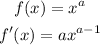
So if we are looking for f'(x) when f(x) = x^2,

`\begin{gathered} f(x)=x^2 \\ f^(\prime)(x)=2x^(2-1) \\ f^(\prime)(x)=2x \end{gathered}`

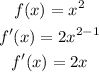
Applying this to our function f(x) = 12x^2, we get:

`\begin{gathered} f(x)=12x^2 \\ f^(\prime)(x)=12(2)x^(2-1) \\ f^(\prime)(x)=24x^1 \\ f^(\prime)(x)=24x \end{gathered}`