Question

A bag contains 6 lemon,3 Apple, and 2 cherry candies.You reach in and take 3 pieces of candy at random.Find the probability that you have 2 cherry candies and 1 lemon candy.

Answer 1

Step-by-step explanation

Since we have 11 total candies, we need to apply the following combinatory in order to know the number of possibilities:

`11\text{ C 3 = 165}`

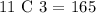
We have 165 different ways to combine the candies.

Since we can just select 2 cherry candies and 1 lemon we need to apply the following relationships:

2 C 2 = 1

We have 1 different way to select two cherry candies.

Then, applying the same reasoning to the lemons

6 C 1 = 6

We have 6 different ways to select one lemon candies.

Multiplying both values:

6*1 = 6 ---> There are 6 different ways to select 2 cherry and 1 lemon candies.

Therefore, the probability is as follows:

`P(2\text{ cherry and 1 lemon\rparen=}(6)/(165)=(2)/(55)=0.036`

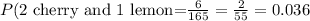
In conclusion, the probability is 2/55 or 0.036