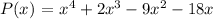1 Answer

Webbower · Answer 1 · 2023-09-25T20:48:49+0000

Question:

the equation of a polynomial to match the dotted graph

Points given (-3,0), (-2,0), (0,0), (3,0)

Solution:

Notice that if P is a polynomial and c is a real number, then the following are equivalent:

1. c is a zero of P.

2. x = c is a solution of the equation P(x) = 0.

3. x- c is a factor of P(x).

4. c is an x-intercept of the graph of P.

Then, due to the above, we can conclude that as -3, -2, 0, and 3 are zeroes of P, the P(x) can be written as:

$P(x)\text{ = (x+3)}(x+2)(x+0)(x-3)$

this is equivalent to:

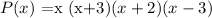
$P(x)\text{ =x (x+3)}(x+2)(x-3)$

In expanded form, this is equivalent to:

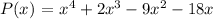
$P(x)\text{ = }x^4+2x^3-9x^2-18x$

then, the correct answer is:

$P(x)\text{ = }x^4+2x^3-9x^2-18x$

Please log in or register to add a comment.