Given the function:
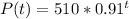
To solve this question, follow the steps below.
Step 01: Find the initial population size.
The initial population size is the population size when t = 0.
Then, substitute x by 0 to find P(0).
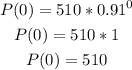
The initial population size is 510 fish.
Step 02: Find it the population size is increasing or decreasing.
To do it, find P(1) and P(2):
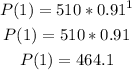
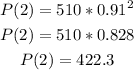
So, P(0) < P(1) < P(2). The population is decreasing.
The function represents a decay.
Step 03: Find the population change per year.
To find the population change, use the formula below:
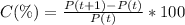
So, comparing P(0) and (P1):
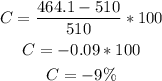
The population decreases by a percent of 9%.
In summary:
- The initial population size is 510 fish.
- The function represents a decay.
- The population decreases by a percent of 9%.