We have the following system of equations:
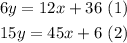
To determine if it has one solution, infinitely many solutions or no solution, let's rewrite the equations in slope-intercept form:

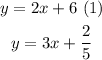
*If the slopes are the same but the y-intercepts are different, the system has no solution.
*If the slopes are different, the system has one solution.
*If the slopes are the same and the y-intercepts are the same, the system has many solutions.
Then, in this case since their slopes are different and their y-intercept are different, the system of equations has exactly one solution.