Question

a. Write x explicitly as a function of p. b. What is the practical domain of the function? c. How many units will be sold at a unit price of 1.50?

Answer 1

(a) x = 3 - p²

(b) (0, ∞)

(c) 750 units [ or 0.75 thousand]

Explanation:

Given the equation:

`p^2+x=3`

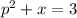
Where:

• x = the annual number of units demanded of a product (in thousands).

,

• p = unit price, in dollars per unit.

Part A

`\begin{gathered} p^2+x=3 \\ \text{Subtract }p^2\text{ from both sides.} \\ p^2-p^2+x=3-p^2 \\ \implies x=3-p^2 \end{gathered}`

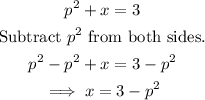
x explicitly as a function of p is x=3-p².

Part B

The domain of the function is the set of all possible values of p.

The price is always non-negative, therefore, the practical domain is:

`(0,\infty)`

Part C

At a unit price of 1.50 i.e. p=1.50

`x=3-p^2=3-1.5^2=0.75`

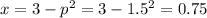
When the unit price is 1.50, the number of units sold will be:

`\begin{gathered} 0.75\text{ thousands} \\ =0.75*1000 \\ =750\text{ units} \end{gathered}`

At a unit price of 1.50, 750 units [ or 0.75 thousand] will be sold.