Question

A certain strain of bugs had a population of 42. One week later the population had then risen to 78.A) Develop the function of the form p = ae^kt that represents the population after t weeks. B) use the function to predict when the population will reach 500.

Answer 1

A)

`p=42\cdot e^(0.619t)`

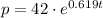
B) week 4

Explanation:

We have that the function has the following exponential form:

`p=ae^(kt)`

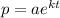
A)

We must calculate the value of k, replacing all the corresponding values, like this:

`\begin{gathered} 78=42\cdot e^(k\cdot1) \\ e^k=(78)/(42) \\ k=\ln \: \mleft((78)/(42)\mright) \\ k=0.619 \end{gathered}`

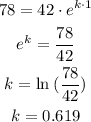
Therefore, the function would be:

`p=42\cdot e^(0.619t)`

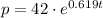
B)

To calculate the time it takes to reach 500, we must plug in the value of p and solve for t, like this:

`\begin{gathered} 500=42\cdot\: e^(0.619t) \\ e^(0.619t)=(500)/(42) \\ 0.619t=\ln \: \mleft((500)/(42)\mright) \\ t=(\ln \: \mleft((500)/(42)\mright))/(0.619) \\ t=4 \end{gathered}`

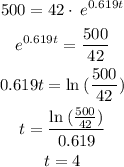
Which means that the population will reach a population of 500 during week 4